算法相关笔记
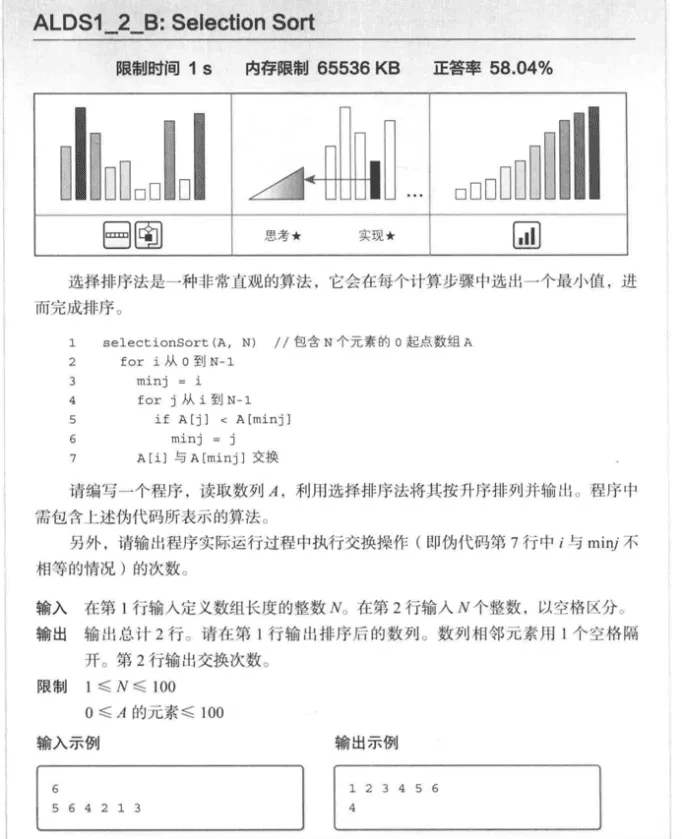
选择排序
实现示例:
C
#include <stdio.h>
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
/* 选择排序 并返回交换次数 */
int selectionSort(int A[], int N)
{
int count = 0, pivot;
for (int i = 0; i < N - 1; i++) {
pivot = i;
for (int j = i + 1; j < N; j++) {
if (A[j] < A[pivot])
pivot = j;
}
// 如果本次循环 pivot刚好是最小值 则pivot不会改变,也就不用交换
if (pivot != i) {
swap(&A[i], &A[pivot]);
count++;
}
}
return count;
}
int main()
{
int A[100], N, count;
scanf("%d", &N);
for (int i = 0; i < N; i++)
scanf("%d", &A[i]);
count = selectionSort(A, N);
for (int i = 0; i < N; i++) {
if (i > 0)
printf(" ");
printf("%d", A[i]);
}
printf("\n%d\n", count);
return 0;
}插入排序

实现示例:
C
#include <stdio.h>
/* 按照顺序输出数组元素 */
void trace(int A[], int N)
{
for (int i = 0; i < N; i++) {
if (i > 0)
printf(" "); // 相邻元素之间留空格
printf("%d", A[i]);
}
printf("\n");
}
/* 插入排序 */
void insertionSort(int A[], int N)
{
int j, v;
for (int i = 1; i < N; i++) {
v = A[i];
j = i - 1;
while (j >= 0 && A[j] > v) {
A[j + 1] = A[j];
j--;
}
A[j + 1] = v;
trace(A, N);
}
}
int main()
{
int N;
int A[100];
scanf("%d", &N);
for (int i = 0; i < N; i++)
scanf("%d", &A[i]);
trace(A, N);
insertionSort(A, N);
return 0;
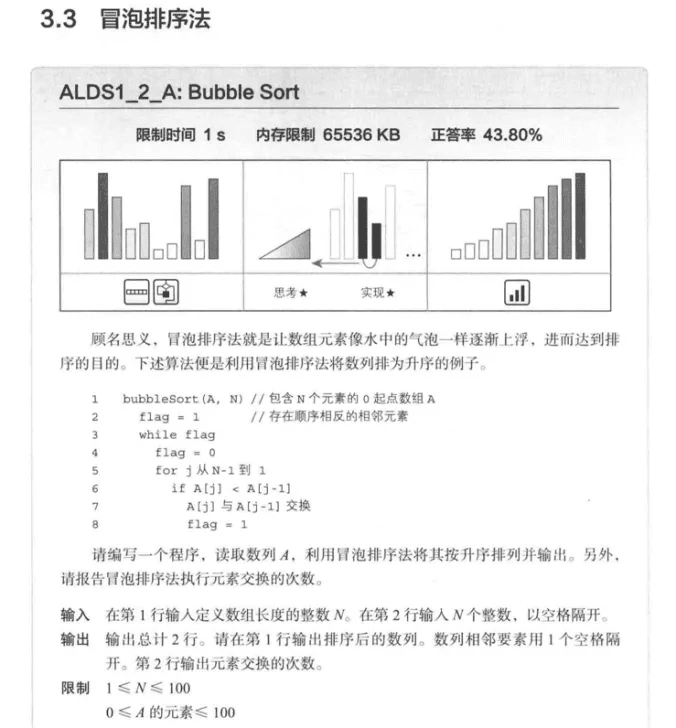
}冒泡排序
实现示例:
C
#include <stdio.h>
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
/* 冒泡排序 并返回交换次数 */
int bubbleSort(int A[], int N)
{
int count = 0;
for (int i = N - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (A[j] > A[j + 1]) {
swap(&A[j], &A[j + 1]);
count++;
}
}
}
return count;
}
int main()
{
int A[100], N, count;
scanf("%d", &N);
for (int i = 0; i < N; i++)
scanf("%d", &A[i]);
count = bubbleSort(A, N);
for (int i = 0; i < N; i++) {
if (i > 0)
printf(" ");
printf("%d", A[i]);
}
printf("\n%d\n", count);
return 0;
}其他排序算法相关
排序算法动画演示:https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html
十大经典排序算法动画与解析:https://blog.csdn.net/dQCFKyQDXYm3F8rB0/article/details/87910210
重点:归并、快排、堆排。
快排是重点中的重点:
排序算法 - 快速排序(4种方法实现)
- https://blog.csdn.net/originalHSL/article/details/131078302
- https://blog.csdn.net/Dreaming_TI/article/details/129427946
- https://blog.csdn.net/v_JULY_v/article/details/6262915
十五大经典算法研究:https://blog.csdn.net/v_july_v/category_9260754.html
最后,再给出一个快速排序算法的简洁示例:
C
void quicksort(int l, int u)
{ int i, m;
if (l >= u) return;
swap(l, randint(l, u));
m = l;
for (i = l+1; i <= u; i++)
if (x[i] < x[l])
swap(++m, i);
swap(l, m);
quicksort(l, m-1);
quicksort(m+1, u);
}如果函数的调用形式是quicksort(0, n-1),那么这段代码将对一个全局数组x[n]进行排序。函数的两个参数分别是将要进行排序的子数组的下标:l是较低的下标,而u是较高的下标。函数调用swap(i,j)将会交换x[i]与x[j]这两个元素。第一次交换操作将会按照均匀分布的方式在l和u之间随机地选择一个划分元素。
原文链接:https://blog.csdn.net/v_JULY_v/article/details/6116297
和MergeSort 比较,QuickSort 的一个巨大优点是它是原地排序的,它反复交换元素, 直接在输入数组中进行操作。由于这个原因,它只需要分配极少的额外内存用于 中间计算。从美学的角度看,QuickSort 是一种引人注目的优雅算法,并且具有 同等优雅的运行时间分析。
用数组实现栈
实现示例:
C
#include <stdio.h>
#include <stdlib.h>
/* 用数组实现栈 */
int top, A[100];
void push(int x)
{
/* 将元素插入top当前位置 top指向下一个位置 */
A[top++] = x;
}
int pop()
{
/* top当前值是未初始化的 返回top前面位置的值*/
return A[--top];
}
int main()
{
int a, b;
top = 0;
char s[100];
while (scanf("%s", s) != EOF) {
if (s[0] == '+') {
a = pop();
b = pop();
push(a + b);
} else if (s[0] == '-') {
b = pop();
a = pop();
push(a - b);
} else if (s[0] == '*') {
a = pop();
b = pop();
push(a * b);
} else {
push(atoi(s));
}
}
printf("%d\n", pop());
return 0;
}图相关的学习笔记
广度优先搜索的特征为从起点开始,由近及远进行广泛的搜索。因此,目标顶点离起点越近,搜索结束得就越快。
深度优先搜索的特征为沿着一条路径不断往下,进行深度搜索。虽然广度优先搜索和深度优先搜索在搜索顺序上有很大的差异,但是在操作步骤上却只有一点不同,那就是选择哪一个候补顶点作为下一个顶点的基准不同。
广度优先搜索选择的是最早成为候补的顶点,因为顶点离起点越近就越早成为候补,所以会从离起点近的地方开始按顺序搜索;而深度优先搜索选择的则是最新成为候补的顶点,所以会一路往下,沿着新发现的路径不断深入搜索。
贝尔曼- 福特(Bellman-Ford)算法是一种在图中求解最短路径问题的算法。最短路径问题就是在加权图指定了起点和终点的前提下,寻找从起点到终点的路径中权重总和最小的那条路径。贝尔曼- 福特算法的名称取自其创始人理查德· 贝尔曼和莱斯特· 福特的名字。贝尔曼也因为提出了该算法中的一个重要分类“动态规划”而被世人所熟知。
与前面提到的贝尔曼- 福特算法类似,狄克斯特拉(Dijkstra)算法也是求解最短路径问题的算法,使用它可以求得从起点到终点的路径中权重总和最小的那条路径路径。
狄克斯特拉算法的名称取自该算法的提出者埃德斯加· 狄克斯特拉,他在1972 年获得了图灵奖。
比起需要对所有的边都重复计算权重和更新权重的贝尔曼- 福特算法,狄克斯特拉算法多了一步选择顶点的操作,这使得它在求最短路径上更为高效。将图的顶点数设为n、边数设为m,那么如果事先不进行任何处理,该算法的时间复杂度就是O( n2)。不过,如果对数据结构进行优化,那么时间复杂度就会变为O(m+ nlogn)。
总的来说,就是不存在负数权重时,更适合使用效率较高的狄克斯特拉算法,而存在负数权重时,即便较为耗时,也应该使用可以得到正确答案的贝尔曼- 福特算法。
A*(A-Star)算法也是一种在图中求解最短路径问题的算法,由狄克斯特拉算法发展而来。
狄克斯特拉算法会从离起点近的顶点开始,按顺序求出起点到各个顶点的最短路径。也就是说,一些离终点较远的顶点的最短路径也会被计算出来,但这部分其实是无用的。与之不同,A* 就会预先估算一个值,并利用这个值来省去一些无用的计算。
A* 算法在游戏编程中经常被用于计算敌人追赶玩家时的行动路线等,但由于该算法的计算量较大,所以可能会使游戏整体的运行速度变慢。因此在实际编程时,需要考虑结合其他算法,或者根据具体的应用场景做出相应调整。
题解:最大利润
C
#include <stdio.h>
#define N 200000
int main()
{
int a[N], num;
scanf("%d", &num);
for (int i = 0; i < num; i++) {
scanf("%d", &a[i]);
}
int imin = a[0];
int imax = a[1];
int ans = a[1] - a[0];
for (int i = 1; i < num; i++) {
// 每次到下标i 更新最大值 以及最大利润
if (a[i] > imax) {
imax = a[i];
ans = a[i] - imin;
}
// 看看最小值是不是要更新
if (a[i] < imin) {
imin = a[i];
}
}
printf("%d\n", ans);
return 0;
}KMP
KMP算法呢可以认为是对BF算法的一个优化,它和BF的算法的区别在于:
KMP 和 BF 不一样的地方在,主串的 i 不会回退,并且子串的 j 也不会每次都回退到 0 号位置。
算法优化效果:O(M*N) -> O(M+N)
不匹配的时候,j回退到哪里?这个是核心。
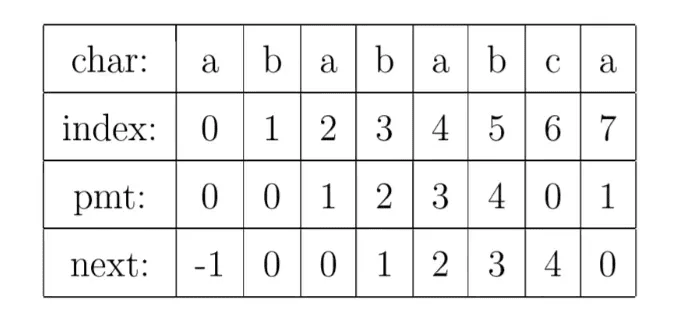
next数组释义:
next数组是一个与模式串(子串)等长的数组,用来存储子串在j位置匹配失败时,要回退的下标位置。
这里下标以0开始计算。
next[0] 代表第一个字符匹配失败,没有回退位置,next[0]设定为-1(其他值也可以,这个值是多少没有意义)。
next[1]匹配失败,唯一能回退的下标就是0,所以next[1]=0。(子串可能是空或者只有一个字符,注意实际场景)。
其它位置,next[j]的计算方法是: j前面相同子串的长度(第j位字符前面j-1位字符组成的淄川的前后缀重合字符数)。
具体释义:
从j-1开始往前寻找两个相同的子串(下标小于j的所有子串不包含j本身,子串是真子串,不包含整个),并且这两个子串必须是前面那个以下标 0 位置的字符开始,后面那个以 j-1 下标位置的字符结尾,这两个子串可以有重叠的部分,但是不能完全重叠(完全重叠就是一个串了)。 然后j回退的位置就是这两个相同子串的长度!
不明白可以参考链接里面的解释。尤其是知乎链接里面的图。
前缀表和next数组定义不一样,不能搞混,可以直接使用next,不用pmt。
知道如何手写next数组,和如何代码实现next数组,完全不是一个种思路。手写很容易,只要按照定义走,代码很不好理解,需要层层递推。这块需要慢慢消化。写出next数组后,还需要进一步优化。kmp主体思路反而比较简单,本质跟bf暴力一样。区别在于回退,也就是next的实现。
流程和代码可以参照以下:


求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。


next数组的理解:

纠正:i<length才对。
学习参考:
- https://www.bilibili.com/video/BV19Q4y1c7ko/
- https://www.bilibili.com/video/BV16X4y137qw/
- https://zhuanlan.zhihu.com/p/115334850
- https://zhuanlan.zhihu.com/p/659483746
- https://www.zhihu.com/question/21923021/answer/281346746
- https://www.zhihu.com/question/394350943/answer/1222971820
- https://blog.csdn.net/qq_43869106/article/details/128753527
- https://cloud.tencent.com/developer/article/2382684
timsort原理学习
Timsort是一种混合稳定排序算法,源自归并排序(merge sort)和插入排序(insertion sort)。
2002年Tim Peters为Python编程语言创建了Timsort。自从Python 2.3开始,Timsort一直是Python的标准排序算法。如今,Timsort 已是是 Python、 Java、 Android平台 和 GNU Octave 的默认排序算法。
本质上 Timsort 是一个经过大量优化的归并排序,而归并排序已经到达了最坏情况下,比较排序算法时间复杂度的下界,所以在最坏的情况下,Timsort 时间复杂度为 O(nlgn)。在最佳情况下,即输入已经排好序,它则以线性时间运行 O(n)。
参考资料:
猜数字游戏
关于随机数
C语言标准库 #include <stdlib.h> rand函数默认种子是1,要设置成随机数,不然每次运行程序,产生的随机数都是一样的。
种子固定,叫做伪随机数的随机数。设置成当前时间的种子是一种选择。


C
/* 生成随机数(其一)*/
#include <stdio.h>
#include <stdlib.h>
int main(void) {
int retry; /* 再运行一次? */
printf("在这个编程环境中能够生成0~%d的随机数。\n", RAND_MAX);
/* rand函数的默认种子是常量1,要每次运行程序结果不同,要改变种子的值 */
do {
printf("\n生成了随机数%d。\n", rand());
printf("再运行一次?··· (0)否 (1)是:");
scanf("%d", &retry);
} while (retry == 1);
return 0;
}C语言规定0以外的值为真,0为假。

最终版本:
C
/* 猜数游戏(其五:显示输入记录)*/
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX_STAGE 10 /* 最多可以输入的次数 */
int main(void) {
int i;
int stage; /* 已输入的次数 */
int no; /* 读取的值 */
int ans; /* 目标数字 */
int num[MAX_STAGE]; /* 读取的值的历史记录 */
srand(time(NULL)); /* 设定随机数的种子 */
ans = rand() % 100; /* 生成0~99的随机数 */
printf("请猜一个0~99的整数。\n\n");
stage = 0;
do {
printf("还剩%d次机会。是多少呢:", MAX_STAGE - stage);
scanf("%d", &no);
num[stage++] = no; /* 把读取的值存入数组 */
if (no > ans)
printf("\a再小一点。\n");
else if (no < ans)
printf("\a再大一点。\n");
} while (no != ans && stage < MAX_STAGE);
if (no != ans)
printf("\a很遗憾,正确答案是%d。\n", ans);
else {
printf("回答正确。\n");
printf("您用了%d次猜中了。\n", stage);
}
puts("\n--- 输入记录 ---");
for (i = 0; i < stage; i++)
printf(" %2d : %4d %+4d\n", i + 1, num[i], num[i] - ans);
// %+4d + 表示显示数字的正负号,来表示跟答案之间的差距。
return 0;
}光标移动字符消失
C
/* 退格符\b的使用示例:每隔1秒消去1个字符 */
#include <stdio.h>
#include <time.h>
/*--- 等待x毫秒 ---*/
int sleep(unsigned long x) {
clock_t c1 = clock(), c2;
do {
if ((c2 = clock()) == (clock_t)-1) /* 错误 */
return 0;
} while (1000.0 * (c2 - c1) / CLOCKS_PER_SEC < x);
return 1;
}
int main(void) {
int i;
printf("ABCDEFG");
for (i = 0; i < 7; i++) {
sleep(1000); /* 每隔1秒 */
printf("\b \b"); /* 从后面逐个消除字符 */
fflush(stdout); /* 清空缓冲区 */
}
return 0;
}
上面的光标移动跟理解中的移动光标不一样,需要\b两次才能跨过一个字符。暂时先记住。
<time.h>中的clock_t ,出错返回(clock_t)-1,强制类型转换


终端显示倒数计时
C
/* 倒计时后显示程序运行时间 */
#include <stdio.h>
#include <time.h>
/*--- 等待x毫秒 ---*/
int sleep(unsigned long x) {
clock_t c1 = clock(), c2;
do {
if ((c2 = clock()) == (clock_t)-1) /* 错误 */
return 0;
} while (1000.0 * (c2 - c1) / CLOCKS_PER_SEC < x);
return 1;
}
int main(void) {
int i;
clock_t c;
for (i = 10; i > 0; i--) { /* 倒数 */
printf("\r%2d", i);
fflush(stdout);
sleep(1000); /* 暂停1秒 */
}
printf("\r\aFIRE!!\n");
c = clock();
printf("程序开始运行后经过了%.1f秒。\n", (double)c / CLOCKS_PER_SEC);
return 0;
}
心算训练
C
/* 心算训练(连加3个三位数的整数)*/
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void) {
int a, b, c; /* 要进行加法运算的数值 */
int x; /* 已读取的值 */
clock_t start, end; /* 开始时间·结束时间 */
double req_time; /* 所需时间 */
srand(time(NULL)); /* 设定随机数的种子 */
a = 100 + rand() % 900; /* 生成100~999的随机数 */
b = 100 + rand() % 900; /* 〃 */
c = 100 + rand() % 900; /* 〃 */
printf("%d + %d + %d等于多少:", a, b, c);
start = clock(); /* 开始计算 */
while (1) {
scanf("%d", &x);
if (x == a + b + c)
break;
printf("\a回答错误!!\n请重新输入:");
}
end = clock(); /* 计算结束 */
req_time = (double)(end - start) / CLOCKS_PER_SEC;
printf("用时%.1f秒。\n", req_time);
if (req_time > 30.0)
printf("花太长时间了。\n");
else if (req_time > 17.0)
printf("还行吧。\n");
else
printf("真快啊。\n");
return 0;
}C
/* 同时训练扩大水平方向视野的心算训练 */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void) {
int stage;
int a, b, c; /* 要进行加法运算的数值 */
int x; /* 已读取的值 */
int n; /* 空白的宽度 */
clock_t start, end; /* 开始时间·结束时间 */
srand(time(NULL)); /* 设定随机数的种子 */
printf("扩大视野心算训练开始!!\n");
start = clock(); /* 开始计算 */
for (stage = 0; stage < 10; stage++) {
a = 10 + rand() % 90; /* 生成10~99的随机数 */
b = 10 + rand() % 90; /* 〃 */
c = 10 + rand() % 90; /* 〃 */
n = rand() % 17; /* 生成0~16的随机数 */
printf("%d%*s+%*s%d%*s+%*s%d:", a, n, "", n, "", b, n, "", n, "", c);
do {
scanf("%d", &x);
if (x == a + b + c)
break;
printf("\a回答错误。请重新输入:");
} while (1);
}
end = clock(); /* 计算结束 */
printf("用时%.1f秒。\n", (double)(end - start) / CLOCKS_PER_SEC);
return 0;
}

输出格式化的总结,挺有意思的。特别是%.s 表示前个字符。
C-Leetcode-30天
学习&做题:
Day 1:
20240528完成。
Day 2:
20240529完成。
Day 3:
动态规划,未完成。
Day 4:
20240529完成。