Learning representations by back-propagating errors
论文在线阅读
中文翻译:通过反向传播误差学习表示
论文介绍
- 发表时间与主要作者:1986年,由David E. Rumelhart、Geoffrey E. Hinton和Ronald J. Williams三位大神级人物共同发表。
- 提出背景与核心问题:在80年代,神经网络领域遇到的最大难题就是如何高效地训练多层网络。传统的感知机只能处理线性可分问题,多层网络虽然理论上更强大,但缺乏有效的训练方法。作者提出反向传播算法(Backpropagation),就是为了解决多层神经网络的高效训练问题。
- 解决效果与量化数据:反向传播算法极大提升了神经网络的训练效率,使得多层网络能够在实际任务中表现出色。论文中通过手写数字识别等实验,展示了多层网络在复杂任务上的优越表现。比如在手写数字识别任务上,多层网络的准确率远超单层感知机。
- 引用量与影响力:截至2024年,这篇论文的引用量已超过6万次,是人工智能领域最具影响力的论文之一。它直接推动了深度学习的复兴,被誉为深度学习的奠基之作。
论文主要内容概括
这篇论文系统地提出并详细推导了反向传播算法。核心思想是:通过链式法则,将输出误差沿着网络反向传播,逐层计算每个神经元的梯度,从而高效地更新权重。
主要内容概括
- 多层前馈神经网络结构:论文首先介绍了多层前馈神经网络的基本结构,包括输入层、隐藏层和输出层。
- 误差函数与目标:定义了均方误差(MSE)作为损失函数,目标是最小化输出与真实标签之间的误差。
- 反向传播算法推导:通过链式法则,推导出每一层权重的梯度计算公式。算法分为前向传播(计算输出)和反向传播(计算梯度)两个阶段。
- 实验验证:作者用手写数字识别等任务验证了算法的有效性。多层网络在这些任务上表现优异,准确率显著提升。
- 泛化能力与收敛性分析:论文还讨论了网络的泛化能力和训练过程中的收敛性问题。
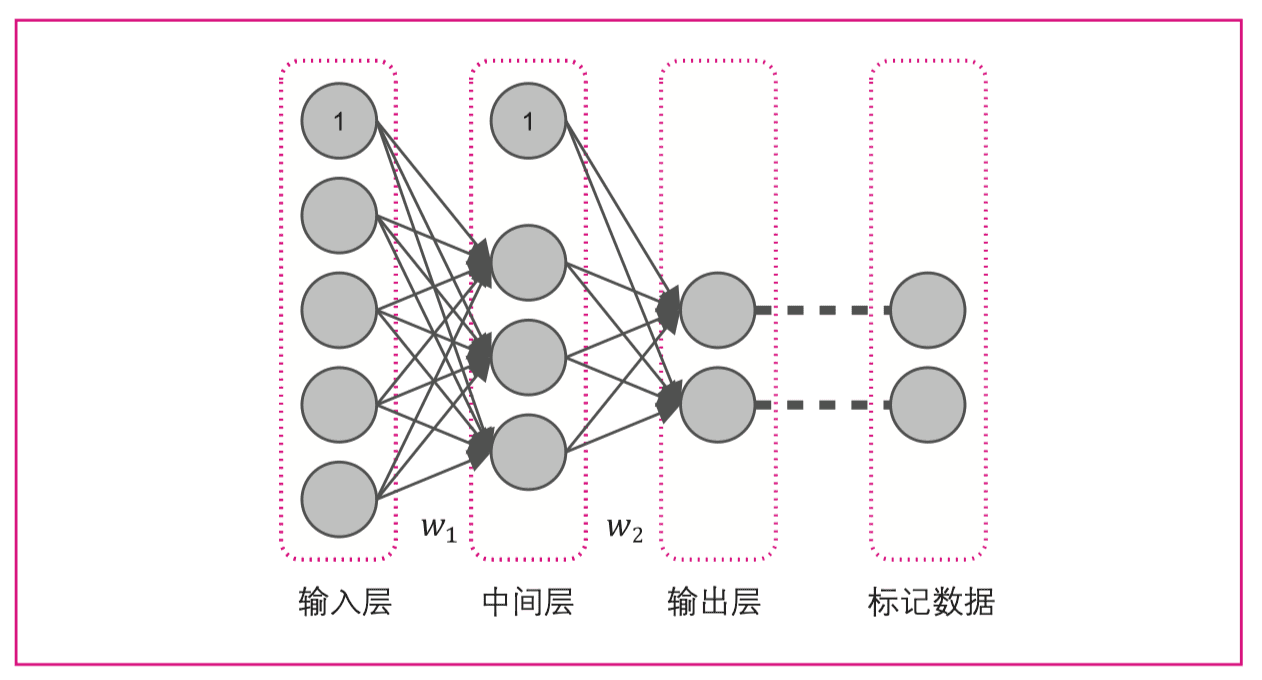
反向传播算法的核心是链式法则的应用。对于一个简单的三层网络(输入层x,隐藏层h,输出层y),权重更新公式可表示为:
输出层权重更新: Δw_{ij} = -η ∂E/∂w_{ij} = η (y_j - t_j) * h_i
隐藏层权重更新: Δw_{ki} = -η ∂E/∂w_{ki} = η [∑(y_j - t_j)w_{ij}] h_i(1-h_i) x_k
其中η是学习率,t是目标输出,E是误差函数。
关键数据
- 在手写数字识别等任务上,多层网络的准确率远高於单层感知机。
- 反向传播算法大幅降低了训练误差,使得神经网络能够拟合更复杂的函数。
历史影响评估
- 算法普及:反向传播成为所有深度学习框架的核心训练算法
- 理论发展:推动了CNN、RNN等网络结构的发展
- 工业应用:奠定了现代AI应用如计算机视觉、自然语言处理的基础
- 引用增长:从1986年的0引用增长到2024年的60,000+引用,年均增长约1,600次
结论
反向传播算法(back propagation)通过调整网络输入的权重系数来降低实际输出与标记数据之间的误差。彻底解决了多层神经网络难以训练的问题,为神经网络和深度学习的发展奠定了坚实基础。它让神经网络真正"活"了起来,成为后续深度学习浪潮的核心技术。没有反向传播,就没有今天的深度学习!这篇论文绝对是AI圈里的"镇馆之宝"。